This blog entry will cover Hypothesis Testing.
What is Hypothesis Testing?
Hypothesis Testing is an experimental tool used to further magnify the impact of a singular factor on a process.
Traditional research involves coming up with hypotheses, followed by getting data from a sample population via surveys or experiments, then followed by calculations and conclusions.
Experiments for multiple factors:
Conduct Experiment > DOE Calculations > Hypothesis Testing > Conclusion
A hypothesis is a statement that researchers use to predict the outcome of an experiment.
Usually, they may only come out with just 1 hypothesis or even a variety.
However, for the hypothesis testing method, we only need to state 2 hypotheses.
These hypotheses stated are mutually exclusive; if we reject one, we automatically accept the other by default
Hence, Hypothesis Testing is a very useful tool to gather a conclusion from an experiment.
Next, I will cover the details and terminology of Hypothesis Testing.*These are crucial for Hypothesis Testing as they involve the basis of understanding how Hypothesis Testing is done.*
Quick recap:
Standard Deviation defines how dispersed the data provided are from the mean.
Ideally, to determine if a statistical hypothesis is true, we have to examine the entire population. However, that is not feasible for populations with large sizes.
To put this into perspective, for example, if you ask "Do humans like chocolate?" Examining the entire population would mean getting data from all 8 billion people in the world. That scale of testing is just not feasible.
Hence, we will need to obtain data from a sample size of the population.
Decision Errors:
There will be trade-offs when taking sample data to estimate the properties of a population since sample data cannot speak for (representative) an entire population realistically, resulting in "Decision Errors".
Two types of errors can result from Hypothesis Testing:
Type I Error:
When a researcher rejects a null hypothesis when it is true.
Probability of committing this error is significance level, Alpha (α)
Type II Error:
When a researcher fails to reject a null hypothesis which is false.
Probability of committing this error is Beta, B
For standard industrial tests, we use a significance level of α = 0.05
Only if consequences of committing a Type I error are severe, such as in health sciences or hospitals, we will then use a significance level of α = 0.01
In the case study task, we will go through the activity according to these steps.For the purpose of product design, we will focus on t-test used for n<30.
Two types of statistical hypotheses:
Null Hypothesis (Ho):
Change in the factor has no significant effect on results, and changes in results are random.
Alternative Hypothesis (H1):
Change in the factor has a significant effect on the results and changes in results are non-random.
Once again, hypotheses stated are mutually exclusive; if we reject one, we automatically accept the other by default
One-tailed:
If Alternative Hypothesis states result due to factor is significantly greater than/lesser than
If Sign of H1 is '<': Left-tailed (-ve)
Significant improvement
If Sign of H1 is '>': Right-tailed (+ve)
Significant deprovement
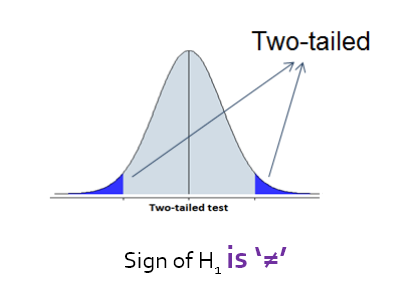
Two-tailed:
If Alternative Hypothesis states result due to factor is significantly different but does not specify whether it is greater/lesser.
When refering to the t-test Distribution chart, it accounts for one-tailed test. Hence, we will have to account for the additional rejectance region.
Hence, we will add half of the significance level into the total significance level.
Therefore, if a test has a significance level of α = 0.05, it will be the 97.5th percentile in the distribution chart for a two-tailed test.
If calculated t is within the acceptance region and does not extend beyond to the rejectance region, we accept the null hypothesis, and vice versa.
t-test Distribution Chart
Ultimately, we use Hypothesis Testing to answer an initial question posed by our research. Hence, in conclusion, we have to backtrack and answer our initial question.
E.g. Does using a unique type of fertiliser significantly improve my crop yield?
Conclusive Answer ㊣:
In conclusion, using the fertiliser will improve crop yield significantly.
NOT ❌:
Hence, we reject H0 and accept H1, H1 is true with a 95% confidence rate.